Celestial Navigation Fundamentals

Angles, angles, angles...

Angles are the most common type of number used by the celestial navigator. The position of the celestial bodies and points on the surface of the earth may be described by angles. The sextant is an instrument that measures angles. Angles are usually measured in degrees, minutes and seconds. The complete circumference has 360 degrees (360°). One degree is equivalent to 60 minutes. The seconds of arc are not used in the celestial navigation, since the angle measurement instrument - the sextant - is not precise enough to measure them. The smallest unit of angle used by navigators is the tenth of minute. Recently, the popularization of GPS devices added the 1/100 of minute.

The nautical mile (=1852 m) is a unit conveniently selected to simplify the conversions between angles and distances. One nautical mile corresponds to an arc of one minute on the surface of earth. Angles and distances on the surface of earth are, therefore, equivalent. One exception is the minute of longitude, equivalent to one mile only near the Earth Equator. Another important equivalence is between time and degrees of longitude. Since the earth goes one complete turn (360°) in 24 hours, each hour corresponds to 15° of longitude. Or 900 Nautical miles (NM).

The Earth and the Celestial Sphere.

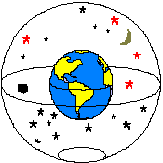Fig. 1 - The Earth and the Celestial Sphere

Imagine that the Earth is the center of the universe and that around the Earth there is a larger sphere, centered in the same point, in which the stars are fixed, as if they were painted in its internal surface. This other ball we call the Celestial Sphere.

To specify a position on the surface of Earth we use a system of coordinates that consists of two angles: latitude and longitude. Latitude is the angle measured from the Equator in direction North-South. Longitude is the angle in the Pole between the Meridian of Greenwich and that of the considered position (fig. 2).

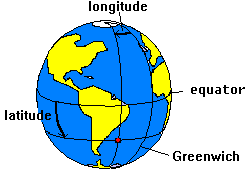fig. 2 - Earth coordinate system

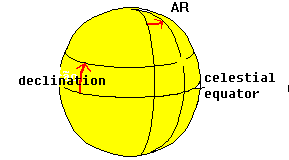fig. 3- Celestial Coordinate System

A similar system is used for the Celestial Sphere. The angle analogous to the latitude in the celestial sphere we call declination. The declination is measured in the plane North-South, from the Celestial Equator. The analog to the longitude is named Right Ascension or RA. Like the longitude, the Right Ascension is measured from an arbitrary Meridian: the Vernal Equinox Point (a.k.a. first point of Aries).

Apparent movement of the stars

The stars have nearly fixed positions in the Celestial Sphere. The Sun, Moon and planets move around during the year, but their movement is slow when compared to the apparent movement due to the rotation of the Earth. So let's consider for now that the celestial objects ( stars, planets, Sun and Moon) are fixed in the Celestial Sphere.

Using the Earth-at-the-center-of-the-universe model, imagine that the Earth is stopped and the celestial sphere is turning around it, completing a turn every 24 hours. You should not be confused by this idea: it's exactly what you observe if you seat and watch the night sky long enough.

The Earth's and Celestial Sphere's axes of rotation are in the same line. Both equators are, therefore, in the same plane (see fig. 1).

The stars, fixed to the celestial sphere, turn around the earth. The celestial sphere poles, being in the axis of rotation, remain fixed in the sky. So, a star located near a celestial pole will appear to be stationary in the sky. That's the case of Polaris, a star that is near the North Celestial Pole (its declination is 89°05' N). It's always in the north direction, a wonderful fact known by every navigator. Unfortunately there's no corresponding bright star near the South Celestial Pole.

Finding the Earth position by observing the stars

Now consider a line connecting the center of a star and the center of the Earth. The point where this line crosses the surface of the Earth we call Geographical Position of this star (or GP). An observer positioned in the GP of a star will see it directly in the vertical, above the head. Since stars move with the celestial sphere, their GPs also move on the surface of the Earth. And they are fast. The Sun's GP, for example, travels a mile every four seconds. The GPs of other stars, closer to the celestial poles, move more slowly. The GP of Polaris moves very slowly, since it's very close to the North Pole.

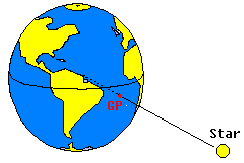Fig. 4- Geographical Position of a Star

Because both Earth and Celestial equators are in the same plane, the latitude of the GP is equal to the declination of the star. The longitude of the GP is known as Greenwich Hour Angle - or GHA - in a reference to the correspondence between hours and longitude.

We can determine, using a Nautical Almanac, the GP of a star (it's GHA and declination) in any moment of time. But we must know the exact time of the observation. As we have seen, 4 seconds may correspond to one mile in the GP of a star. This shows the importance of having a watch with the correct time for the celestial navigation. The Beagle - ship of Charles Darwin's travel in 1830 - carried 22 chronometers on board when she went around the globe in a geographic survey.

Zenith

Another important point is the Zenith. The Zenith is the point in the celestial sphere located in the vertical, over the head of the navigator. The line that connects the Zenith and the center of the Earth crosses the surface in the position of the navigator, the one we want to find. So, we have the following correspondence between points: Surface of Earth Celestial Sphere Geographical Position of a star Center of the star Position of the navigator Zenith

In the figure 5, the GP of the star is represented by X and the Zenith by Z. The distance XZ, from the GP of the star to the point Z of the navigator is called Zenith Distance. This distance, as we have seen, can be expressed in miles or degrees, since it's an arc on the surface of the Earth.

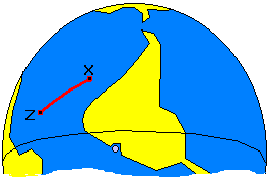fig. 5 - GP of a star and the Zenith

The angle that XZ makes with the True North (i.e. the "bearing" of the star) is called Azimuth ( Az ) (fig. 6).

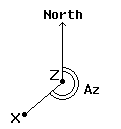fig. 6 - Azimuth of a star

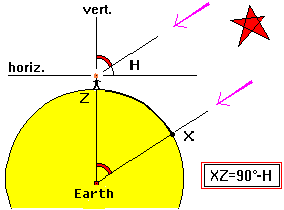fig.7 - Altitude and Zenith distance of a star

The stars are at a great distance from the earth and so the light rays coming from them that reach the Earth are parallel. Therefore, as illustrated in the figure 7, we may say that the distance XZ (as an angle) is equal to the angle that the navigator observes between the star and the vertical. This is important. The distance XZ, measured as an angle, is equal to the angle that the navigator observes between the star and the vertical.

However, it's difficult to determine the Zenith distance with precision, since it's difficult to find the vertical direction in a rocking boat. It's a lot easier to measure the angle between the star and the horizon. This important angle for the celestial navigator is called altitude (H) of the star. The altitude of a star is taken with the sextant held in the vertical plane, measuring the angle between the horizon and the star. In the fig. 7, we can see that the zenith distance equals 90° less the altitude of the star.

We have seen how to determine the zenith distance of a star using the sextant. The Zenith Distance and the GP of a star, however, are not enough to determine our position. With this data we can only say that our position is in a big circle, with the center in the GP of the star and radius equal to the Zenith Distance. This is known as the Circle of Position. Figure 8 shows a Circle of Position. Point X is the GP of the star.

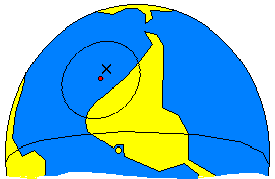fig.8 - Circle of Position

Any observer located on this circle will see the star at the same altitude, but with different Azimuths. In the example of the figure, suppose the navigator observes the star with an altitude of 65°. As we have seen, the Zenith Distance is 90°-H, or 25°. To determine this distance in miles, we multiply by 60, since one degree is equal to 60 nautical miles (NM). So, the Zenith Distance in the example - the radius of our circle - is 1500 NM.

If we just could determinate the exact direction where the GP of the star is - it's Azimuth - that would establish where in the circle we are. How about using a compass? Unfortunately, the compass is not precise enough for celestial navigation. One error of just 3°, common when reading a compass, corresponds to 78 miles of error in our example! Not an acceptable error.

The way to find our position is to draw two or more circles - for two or more celestial bodies - and see where they intercept each other. But drawing these big circles would require really big charts! We work around this problem by making a guess at our position. No matter how lost we are, we can always make a guess. Using this assumed position we can calculate expected altitude for the star at a given time (using the Nautical Almanac).

This Calculated Altitude can then be compared with the Observed Altitude (the actual altitude, measured with the sextant). The difference is the error of our assumed position ( also known as Delta ) in the direction of the star. The Delta can be towards the star or away from it.

>> Click here for the next page

>> Homepage