The time and the lunar calculation It is not much of a problem to keep the time today. We can keep it using a cheap - and yet good - quartz watch. We can get it from the Internet, from a GPS receiver or from all kinds of radio and cell phone devices. But keeping the time was a nightmare for many centuries. Primitive mechanical clocks worked poorly on land and even more so on sea conditions. Temperature variation conspired to change the dimensions of clocks pendulums, making the time pass slower when hot. Lubrication of mechanisms influenced their pace. The problems seemed so complex that at one point even clever fellows, like Isaac Newton, though it was impossible to built a reliable clock to use on the sea. Why is it so important to know the correct time on a boat ? It is because the time is necessary to calculate the longitude using celestial navigation. If the navigator doesn't know the correct time, the boat is basically lost. Of course latitude can be obtained, but longitude cannot. This problem caused many accidents in the past. Captains had to make blind decisions regarding navigation. Entire fleets of ships run into rocks, killing hundreds of sailors and sinking fortunes. At some point it started to damage national economies. Kings tried to direct scientific efforts to solve the problem of longitude determination at sea, by supporting astronomy research and offering large prizes for a workable solution. One of the early scientists to think about the time problem was Galileu Galilei. He suggested that the pendulum could be used as a clock (for the period of a pendulum swing is constant, no matter the amplitude). He also noticed, using the newly invented telescope, that the moons of Jupiter had a fast speed and could be used as clocks in the sky. But observing the jovian moons with the telescope proved to be difficult, even on land. Another larger moon was available: our own. So the quest for the method to find the time using the Moon was started: the search for the perfect lunar based time calculation.
How good is your sextant ? Every celestial navigator dreams with a shinning metal sextant, solid is a rock, with a clear eyepiece and a perfectly divided scale. No perceptible construction error along the arc all the way to 120 degrees. Such things exist, but can be expensive. There are cheaper options: plastic, paper and even do-it-yourself sextants. Even the best instrument has to be checked from time to time. This can be done using the distances between two celestial objects. By taking many different distances and comparing to the Nautical Almanac derived values, we can draw a chart of the sextant error as a function of the angle. This can be used to correct the sextant construction errors (not the index error) and improve the precision of any instrument. The calculation and corrections Most of the work in celestial navigation goes to correct the sextant angle from a number of optical factors. These corrections are supposed to clear the sextant reading from apparent effects and bring it to the same assumptions of the Nautical Almanac. The Nautical Almanac lists the geocentric positions of celestial objects at fixed time intervals (hourly for Sun, Moon and planets, each 3 days for stars). All coordinates refer to object centers. The Almanac is an animated map of geometric points that represent the positions of objects in the celestial sphere. Sextant corrections are familiar to celestial navigators: index correction, height of the eye, refraction, parallax and semi-diameter (more details on corrections) . To understand the way corrections are worked in Lunars and object distance calculations, it's convenient to draw a distinction between two classes of optical factors: those that affect the apparent position of the object and those related to the observer position or instrument peculiarities. Refraction and parallax work to displace the object from its theorical Nautical Almanac place, producing the apparent image, different from the real. This "real' means the theorical universe model used by the Almanac, where objects are points and there is no air. These two factors move the apparent image along the vertical plane: the plane were altitudes are inscribed. The refraction error is caused by light rays "bending" while crossing the multiple air layers. It is a tricky correction, because it depends on atmospheric conditions on the different air layers. The best thing is to avoid too much refraction, by selecting objects with altitudes larger then 20 degrees. The refraction correction calculation uses the following variables: altitude, temperature and pressure.
The correction we must use is the Parallax in Altitude. It is the parallax observed when the object is at some altitude. This can be calculated with the formula: Par. in altitude = Horizontal parallax * Cos(altitude) Both apparent corrections share their dependency on altitude. This leads to a circular dependency inside the calculation: the corrections depend on the altitude, which depends on the corrections. Among all corrections one must be noticed, because it is so large: the Moon parallax. Since the Moon is very close to the Earth, the Moon Parallax can be almost a full degree. The Height of the eye (Dip) does not apply to object distances, since it corrects the position of the sea horizon, not used when distance between two objects is measured. It will be necessary only when handling the two objects altitudes (also required in this calculation). The Index Correction applies to any sextant reading. Semi diameter (SD) are only considered to the Sun and Moon. Other objects are basically points, with no visible dimension. While for altitude readings we talk about lower and upper Limb, with object distance we use the terms near and far limb. If the near limb is used when observing the Sun or Moon, we must add the semi diameter. If the far limb is used, the SD must be subtracted. We must consider yet another correction for the Moon. The Moon is pretty close to the Earth. The linear distance Earth-Moon is about 360.000 Km, and the earth radius is about 6.000 Km. So, the observer is 6000 km closer when the Moon is high in the sky. As a consequence, the Moon disc is a little larger than the Almanac listed geocentric number for the semi diameter. This augmentation of the Moon semi diameter can be as much as 0.2 minutes of arc. It is small, but relevant in this case, since the Lunar calculation requires maximum precision. The order of calculations is:
The cleared Distance can be compared with calculated distances obtained using Almanac tables. Since the Almanac lists object positions for full hours, we must interpolate the time inside the one hour interval that includes the cleared distance. A linear interpolation is used. Measuring the angular distance
|
||||||||||||||||
|
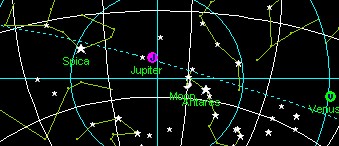
Each Distance between objects calculation - including Lunars- involves measuring three angles, nearly at the same time:
You may be wondering "how can I take the three readings simultaneously ?". Note that the altitudes in this method are only used to calculate the corrections, to clear the distance. A small error in altitudes will not influence the final result significantly. So work the altitudes fast. The distance reading itself is much more important and should be done with great care. You may take the altitudes again after that and average with the first ones.
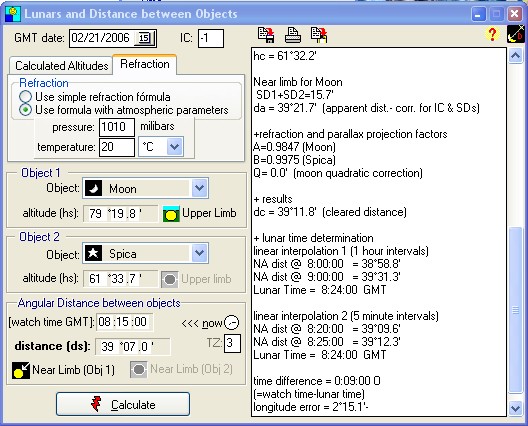
Using the Navigator Lunar Calculator * * this feature is available in Navigator 4.5 SP1 and newer The image below shows the Navigator Lunars calculator. This window can be accessed from the Celestial Navigation form. Click the tab "Other.." and click the "Lunars and Distance between objects" button. The form shown below appears. Select the two objects from the Object combo boxes. This form can both calculate:
If one of the selected objects is the Moon, the calculator switches to Lunar mode automatically. Enter the lunar distance date and IC (index correction). The observation time is optional (after all, this is what we are trying to find with the lunar calculation). The time is used to calculate your "watch error". Input the altitudes for both the Moon and celestial object of choice (in this case, Spica). If you are just playing with Lunars in your backyard, know your position and don't want to take the altitudes, you may input the position and let the program calculate the altitudes for you. In this case, click [Pre calculate altitudes] and choose to paste the altitudes to the corresponding fields.
Input the sextant observed distance and select the limb type for both objects (only necessary for Sun and Moon). Click the "Calculate" button. The program will calculate the Lunar time and clock error. When the object is close to the Moon, the distance change rate is not rellay linear in the one hour interval. So thge program does another 5 minute interpolation, to refine the result. The report to the right of the form contains the calculation in full detail. The relevant results are the Lunar Time and the time correction to be applied to your watch ( if you have one. this method can be performed even without a watch).
|
||||||||||||||||
ęCopr 92-2012 Omar F. Reis - All rights reserved