|
level
of difficulty |
beginner
|
intermediate |
advanced |
Navigator celestial calculation methods
Most of the algorithms used in Navigator software come from 3 sources: the book "Astronomical Algorithms" by Jean Meeus, the Almanac for Computers (US Naval Observatory - 1992) and Bowditch (The American Practical Navigator). An effort was made to keep the navigation workflow as close as possible to the traditional techniques, without the use of computers.
1) Calculation of celestial body positions: Right
Ascension (RA) and declination (Decl)
1.1) Sun - Positions calculated using the VSOP 87* theory, with accuracy within 0.2'.
1.2) Stars - Starting from Nautical Almanac positions on 1/1/1993 00:00:00 UT, positions calculated by adding the effects of precession, nutation and aberration. The effects of proper movement of stars are also considered (starting with version 4.5 of Navigator, read more about the issue here >> ). Star positions are precise when compared to planets and the Moon. The accuracy is within 0.2'. Positions valid from 1900 to 2100.
1.3) Planets - Planets have by far the most complicated calculation method of all celestial bodies. Calculated the rectangular heliocentric coordinates of the planet and the Earth, using numerical series (VSOP 87 theory*). Then added the apparent effect of the time of propagation of the light and calculated the geocentric coordinates, adding the effects of nutation and aberration. Accuracy within 0.6'.
( * Variations Séculaires des Orbites Planétaires 87 - French planetary theory by Bretagnon and Francou of the Bureau des Longitudes of Paris. This method is described in the Meeus book ).
1.4) Moon - The coordinates of the Moon were calculated by formulas, which gives an accuracy within 0.2' ( In versions prior to Oct./2001, this accuracy was within 0.7')
1.5) GHA of celestial bodies is calculated using the formula GHA=15* (GAST-RA) , were :
GAST (Greenwich Apparent Sidereal Time) calculated with
approximated formula.
Precision within 0.2 sec.
1.6) Universal Time (UT) to Dynamical Time (TD) difference calculated by a combination of tables (from 1620 to 1992), actual values (from 1992 to 2001), short term predictions (from 2001 to 2016) and prediction formula (after 2016 and before 1620).
2) Solution of the position triangle PXZ
Position triangle PXZ is an spherical triangle and the solution requires the use of spherical trigonometry formulas (law of sines and law of cosines). read more>>
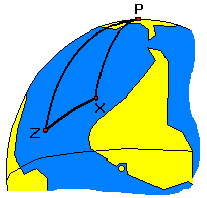
3) Calculated Altitude and Azimuth:
|
Calculated altitude Hc: Calculated Azimuth Az: were: j : Latitude of observer |
4) Corrections to the Instrumental Altitude
Hc = Hi + TC
TC = IC + Dip - R + SD + Par
were:
TC: Total Instrumental altitude correction
Hc : Corrected altitude
Hi : instrumental altitude
IC : Instrumental correction (Index Error)
Dip: Correction relative to the height of the eye is calculated with the
formula:
|
|
Dip = -0.97 * Sqrt(h/0.3048))
Dip in minutes. |
| Some users correctly noted that the factor in the formula deduced using trigonometry differs significantly from -0.97. I can only speculate that this is related to refraction correction, but I'm not sure. This formula is described in the Almanac for Computers (USNO) and I use it because does agree well with the Nautical Almanac table, which is my preferred benchmark. |
Starting with version 4.5, I added support for Dip Short observations, for land navigation. I used the formula from Bowditch.
R: Atmospheric refraction (calculated with approximate formulas, depending on the body altitude) . Staring with version 4.5, I added a more flexible formula, that takes atmospheric parameters (temperature and pressure)
SD: Semidiameter (Calculated for the Moon and Sun and
0 for planets and stars)
Par: Parallax in altitude - Horizontal Parallax calculated for the Moon and planets, from the computed geocentric position. Parallax in altitude computed using the apparent altitude.
5) Solution of the Astronomical Position (AP)
|
For each LOP (Line of Position):
were: |
The equation of the LOP i in the
plane can be expressed by:
Lat = ai * Lon + bi
ai = - cos (LatQ) / tan Azi
bi = LatQ + Lon Q * cos (LatQ) / tan Azi
Factor Cos(LatQ) makes the conversion between horizontal Nautical Miles
and minutes of longitude.
Make the intersection of each two lines i and j
LatX = ( bi . aj - bj . ai
) / ( aj - ai)
LonX = ( LatX - bi ) / ai
were X is the point of intersection.
The astronomical position is found using the average of all the LOPs intersections, as follows:
L= Sum ( Lij . cos aij ) / Sum( cos aij
)
for every i different from j, were L is the Latitude or Longitude. The
use of the factor (cos a) gives smaller importance to intersections of
LOPs forming small angles between them.
Bibliography
| >> "Astronomical Algorithms"
by Jean Meeus ISBN 0943396611 - Willman-Bell |
|
||
| Complete positional calculation methods for stars, planets, Sun and Moon. Accurate descriptions, with many examples. Excellent book for any astronomy programmer. | |||
| >> "Astronomical Formulae
for Calculators" by Jean Meeus ISBN 0943396220 - Willman-Bell |
|
||
| Simple positional astronomy formulas, easy to program on pocket calculators or personal computers. | |||
|
>> Almanac for Computers - 1992 publication
by the US Naval Observatory, with simple formulas for the Sun.
Also good source for sextant corrections. |
||
|
>> HP 65 Math Pack 1 documentation
- Geodesic formulas |
ęCopr 92-2012 Omar F. Reis - All rights reserved
